Measurement of Point Elasticity

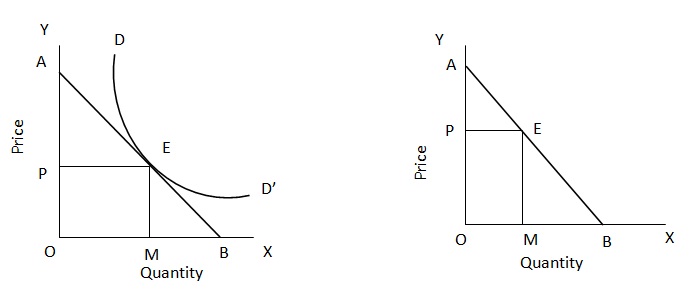
To measure elasticity of demand at point E on the demand curve DD’ we draw a tangent AB through the point E, meeting OY at A and OX at B. the elasticity at the point E is measured by the ratio of EB to EA, i.e. EB /EA. In other words, for any point on the demand curve, the elasticity is measured by the length of the tangent below the point divided by the length above the point.

We can prove that on any point such as E, on a straight line demand curve AB, the elasticity of demand
E_P = Line segment below that point /Line segment above that point = EB/EA.

To prove this, we take a straight line demand curve AB and make a point E on this line AB. Now, we have to show that elasticity at point E is equal to EB /EA. The formula for measurement of elasticity of demand is

E_P = (-) ∆Q /∆P. P0 /Q₀.

Let us ignore the minus sign and find out values of these variables.

From ∆P = OP – O = OP
∆Q = OB – OM = MB
E_P = (-) ∆Q /∆P. P₀/Q₀

Putting these values in the formula
E_p = MB /OP. OP /OM
Or, E_P = MB /OM or MB / PE

Now, since ∆ APE and ∆ EMB are similar, ratio of their sides must be equal. Thus,
MB /PE = ME/PA = EB/EA

It follows that elasticity at point E = EB /EA, i.e. line segment below E divided by line segment above E.
Similarly, elasticity at point E is also equal to
ME /PA or OP/PA. (:. ME = OP)

This formulation will be used in discussing point elasticity on parallel demand curves and intersecting demand curves in discussions to follow.